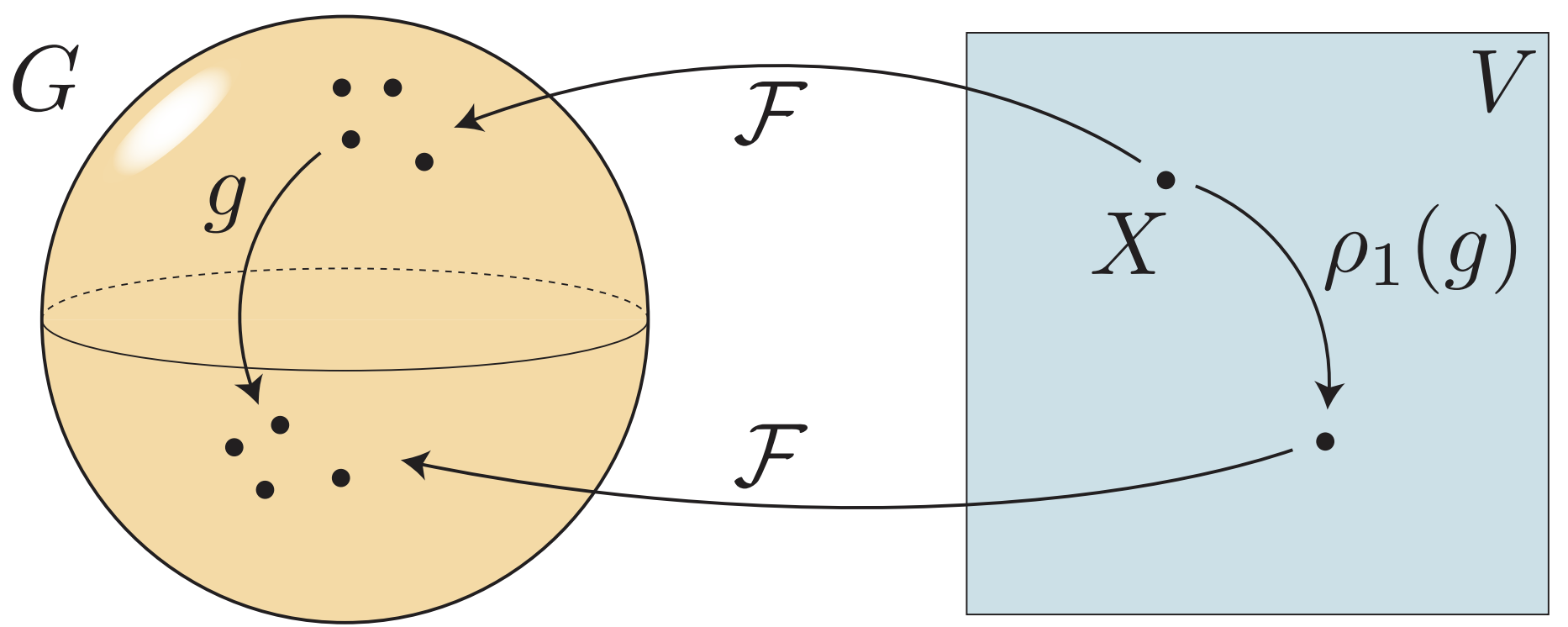
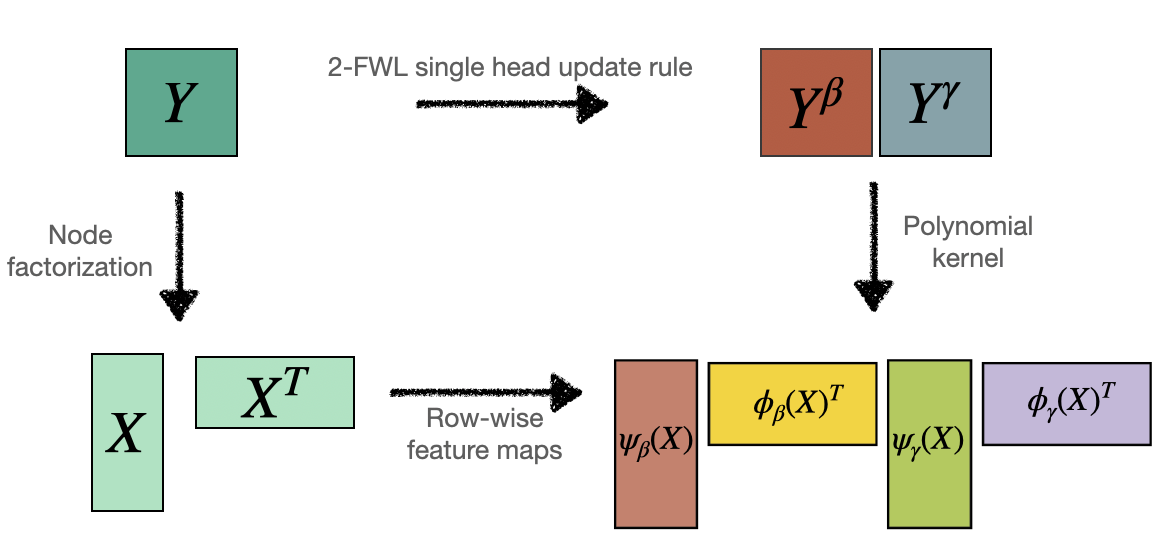
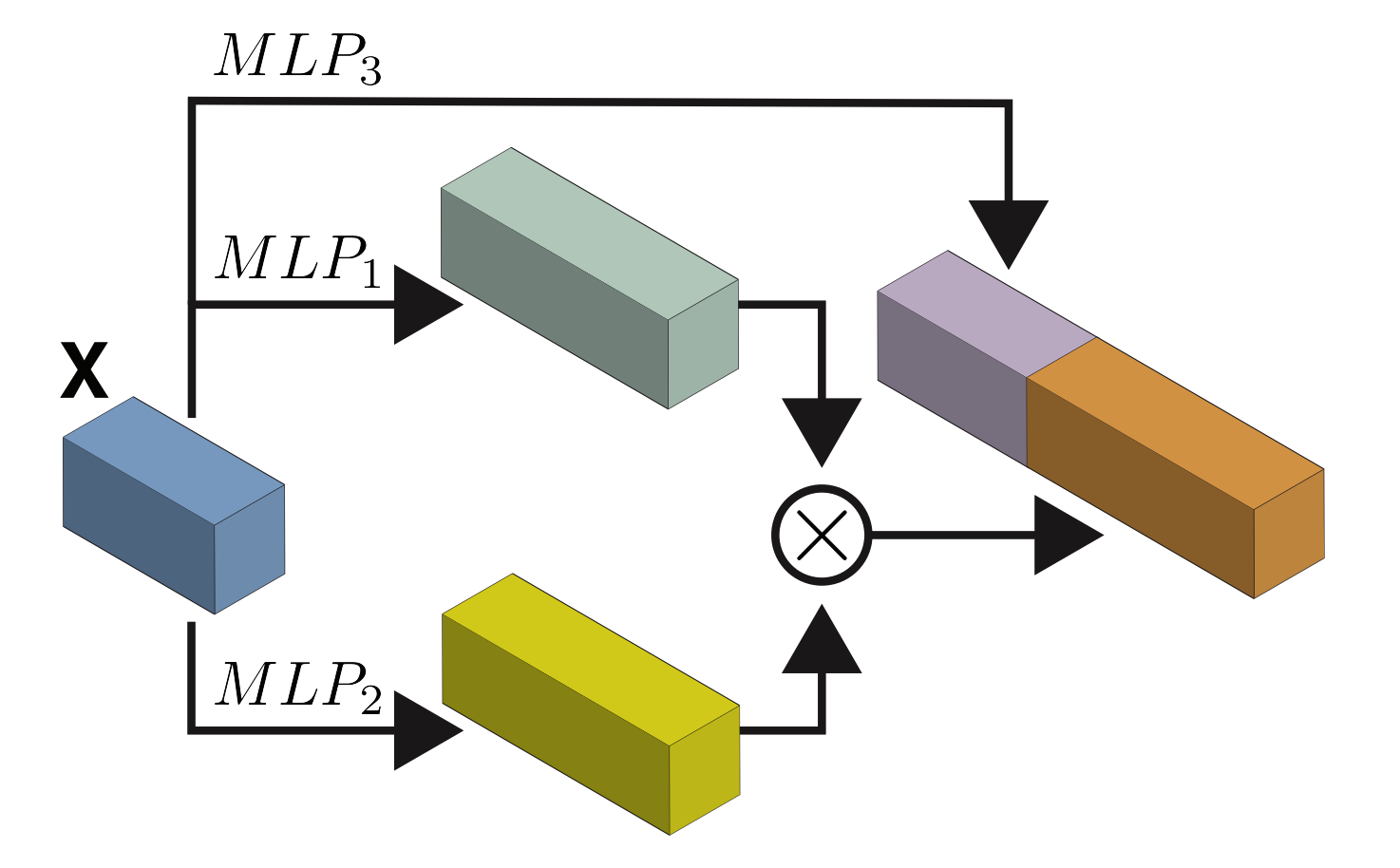
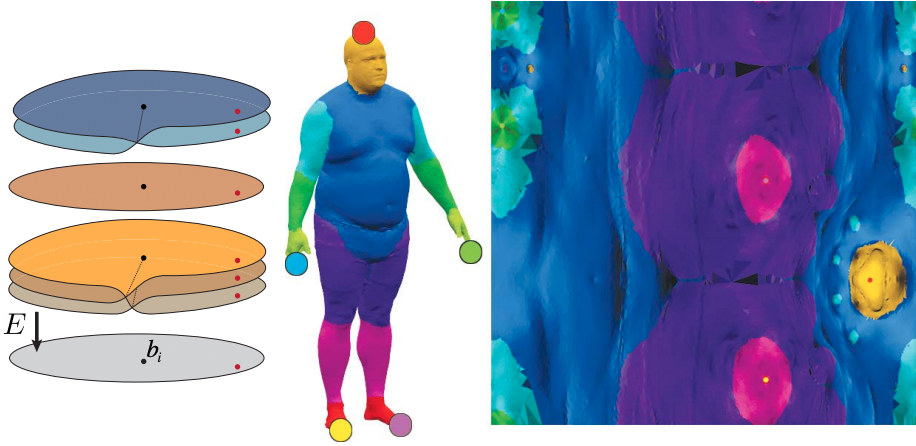
This paper introduces a 3D shape generative model based on deep neural networks. A new image-like (i.e., tensor) data representation for genus-zero 3D shapes is devised. It is based on the observation that complicated shapes can be well represented by multiple parameterizations (charts), each focusing on a different part of the shape. The new tensor data representation is used as input to Generative Adversarial Networks for the task of 3D shape generation. The 3D shape tensor representation is based on a multi-chart structure that enjoys a shape covering property and scale-translation rigidity. Scale-translation rigidity facilitates high quality 3D shape learning and guarantees unique reconstruction. The multi-chart structure uses as input a dataset of 3D shapes (with arbitrary connectivity) and a sparse correspondence between them. The output of our algorithm is a generative model that learns the shape distribution and is able to generate novel shapes, interpolate shapes, and explore the generated shape space. The effectiveness of the method is demonstrated for the task of anatomic shape generation including human body and bone (teeth) shape generation.
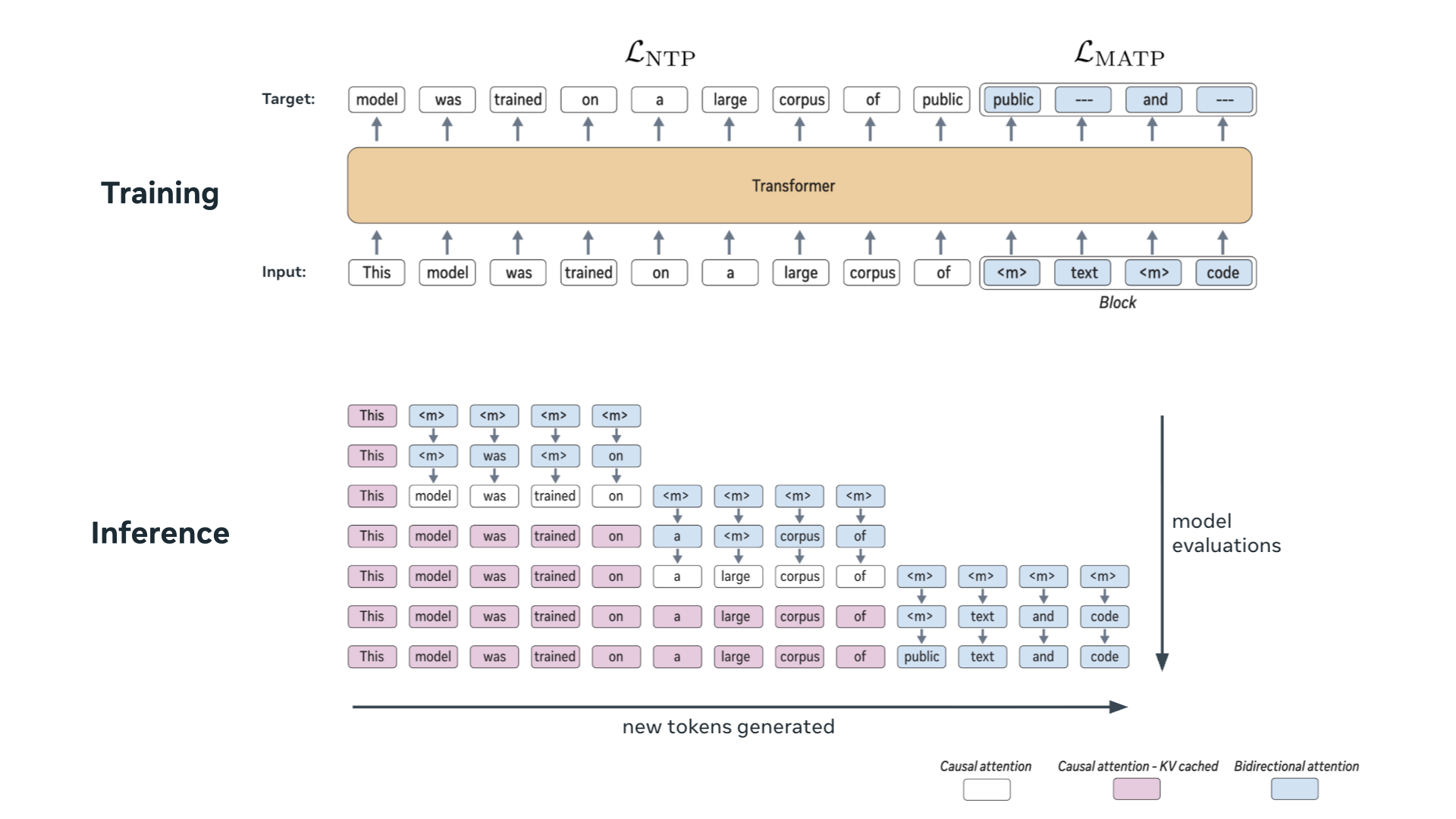
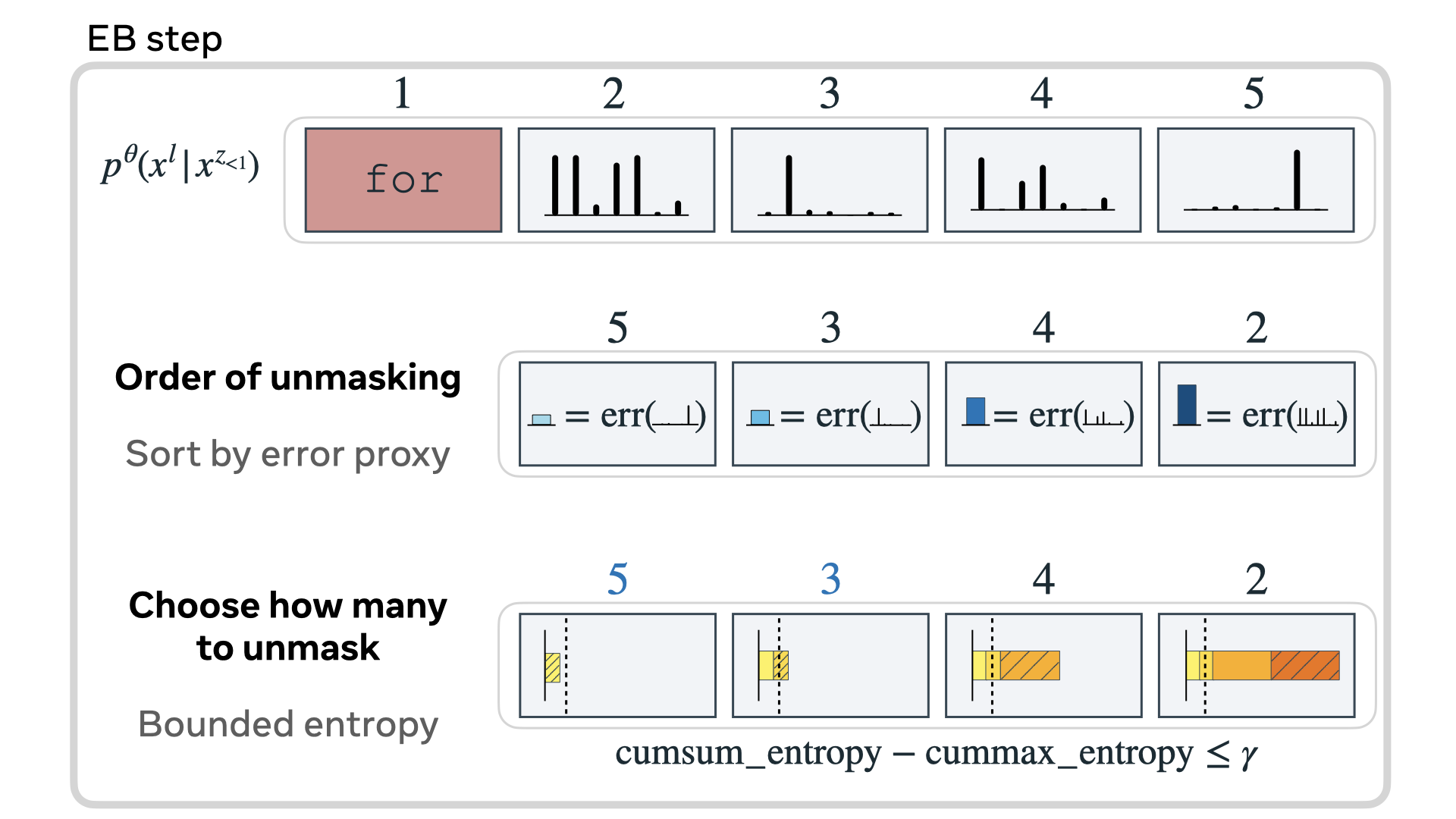
Autoregressive next token prediction language models offer powerful capabilities but face significant challenges in practical deployment due to the high computational and memory costs of inference, particularly during the decoding stage. We introduce Set Block Decoding (SBD), a simple and flexible paradigm that accelerates generation by integrating standard next token prediction (NTP) and masked token prediction (MATP) within a single architecture. SBD allows the model to sample multiple, not necessarily consecutive, future tokens in parallel, a key distinction from previous acceleration methods. This flexibility allows the use of advanced solvers from the discrete diffusion literature, offering significant speedups without sacrificing accuracy. SBD requires no architectural changes or extra training hyperparameters, maintains compatibility with exact KV-caching, and can be implemented by fine-tuning existing next token prediction models. By fine-tuning Llama-3.1 8B and Qwen-3 8B, we demonstrate that SBD enables a 3-5x reduction in the number of forward passes required for generation while achieving same performance as equivalent NTP training.